En serio, ¿tanto han cambiado las mates para que “la resta de toda la vida” ya no sea “la resta de toda la vida”?
Si las letras E, G y B no te suenan a marca de lavadora, al último modelo de móvil o a un colectivo es porque:
- Ya tienes más de 40
- Probablemente peinas canas
- Puede que tengas hijos en E.P.
E.P es como se llama ahora a lo que llamábamos antes E.G.B. La cuestión es que la E.G.B abarcaba entre los 6 y 14 años y la E.P entre los 6 y 12 años (esta matización puede parecer un dato con poca importancia, pero, realmente, tiene mucha, aunque eso puede ser tema para otra ocasión).
Hoy venimos a hablar de que: ¡Ya no se aprende como antes! Resulta que como diga eso de “y me llevo una” o “cero al cociente y bajo la cifra siguiente” o “dividir es repartir” puede que esté estropeando las conexiones neuronales que se deberían producir alegremente en la cabeza de mi chiquillo.
¡Horror, soy un padre mataconexiones! ¡Soy un neuronicida! Yo que solo quería enseñarle a restar para que ganara en seguridad y echarle una manilla con las mates y, al pobre, por poco me lo cargo… Ufff, menos mal que he parado a tiempo y, ahora, por fin, mi niño, desde la libertad que le confiere su condición de ser humano y desde el respeto que yo, como progenitor, le tengo, podrá desarrollar adecuadamente su construcción del pensamiento lógico-matemático.
Dejando la ironía a un lado diremos que:
- Restar era restar
- Restar es restar
- Restar será restar
Ahora bien, “en nuestros tiempos” se priorizaba la mecánica algorítmica por encima de la comprensión. La velocidad en el cálculo por encima de la contextualización. El cálculo por repetición y sin contexto (todos recordamos esas interminables páginas de cálculo de unos cuadernillos muy populares) por encima del cálculo como medio o herramienta para…
La ciencia, a día de hoy (mayo de 2022), ya confirma las teorías del aprendizaje que desde los años 60 (y antes) se venían comentando al respecto de cómo aprende el cerebro (cositas que decían Piaget, Bruner, Vigotsky, Skemp, Dienes…) y, entre otras cosas, se hablaba de algo que se conoce como el proceso “C-P-A” que se traduce como “Concreto-Pictórico-Abstracto”.
Esto quiere decir que aprendemos desde lo concreto y que las transmisiones sinápticas se ven favorecidas cuando la matemática parte desde la manipulación de materiales. Y resulta (y ya nos metemos en la resta) que se supone que trabajar desde lo concreto tiene como finalidad poder comprender, desde el establecimiento de relaciones, qué pasa al restar (hoy nos meteremos solo en restar como acción de quitar una parte de un conjunto total).
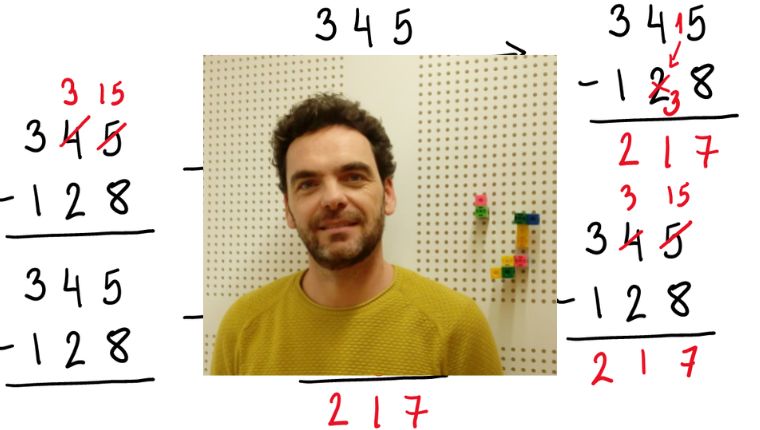
Así resolvíamos muchos de nosotros (los de la EGB) una resta de esas que llamábamos “con llevadas” o “llevando”:
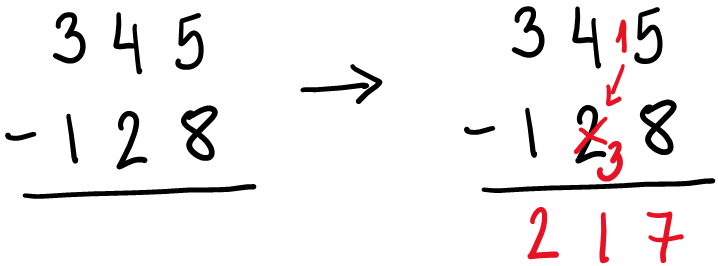
Y decíamos algo como: “Del 8 al 5 no puedo así que voy del 8 al 15. Del 8 al 15 van 7 y me llevo una y se la sumo al de abajo así que ya no hay 2 decenas sino que hay 3. Del 3 al 4 va 1. Del 1 al 3 van 2.”
Esta mecánica de la resta “de toda la vida” es justamente eso, mecánica”. Claro que tiene su explicación pero… ¿Está en disposición un niño de 2.ºEP (que es cuando se inicia en estas cosillas) de comprender por qué motivo el 5 ya no es 5 sino 15 y el 2 ya no es 2 sino 3?
Pues bien, cuando se parte de lo concreto (recuerda, el proceso C-P-A) y se facilitan materiales adecuados que mantienen proporciones en la cabecita del niño ocurren pequeños “¡eureka!” todo el rato.
Este sería el proceso para resolver 345 – 128 que seguirían los niños en los que se ha priorizado la comprensión del cálculo por encima de la mecánica. El material que aparece dibujado son bloques de base 10 que permiten que el alumno pueda realizar cambios y comprobar “cosas” por comparación y superposición (en lugar de creerse cosas, sin más). Es como si fuera a “pedir cambio”. Yo también lo llamo “el trato justo”. Si te doy una barra de estas, ¿qué me das a cambio para que el trato sea justo? Si me das una placa de esas cuadradas, ¿qué te doy a cambio para que el trato sea justo? Aquí va el proceso de la resta (como acción de quitar) de los hijos de la E.G.B:
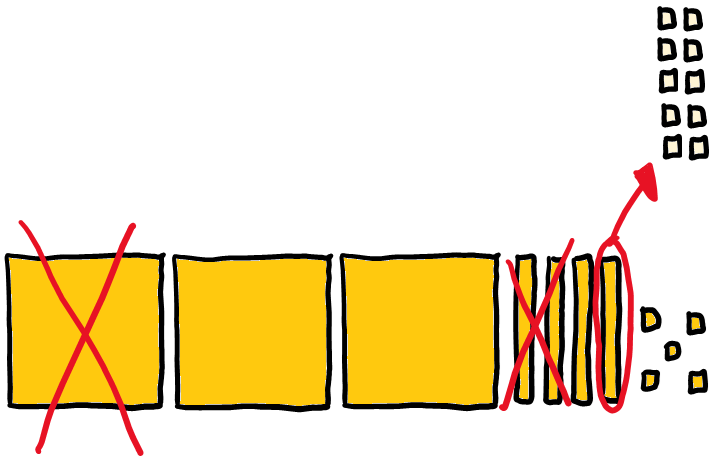
- Representamos la cantidad con nuestros bloques (345):

2. Tenemos que quitar 128. Es decir, tenemos que quitar 100 y 20 y 8. Parece fácil quitar 100 (una placa). También quitar 20 (2 barras) pero, ¡ops! Tengo que quitar 8 “unos” pero solo tengo 5 piecitas de unos. Y aquí es donde viene la importancia de dejarles manipular.
Si han construido el número con materiales, dominan perfectamente qué es 1, qué es 10, qué es 100 y, sobre todo, qué relaciones se establecen entre ellos. Así que no tardan en decir: ¡Cambio una barra por 10 cubitos! Y ocurre esto:
3. Ahora ya puede proceder a quitar los 8 “unos” porque… ¡ya tienen!
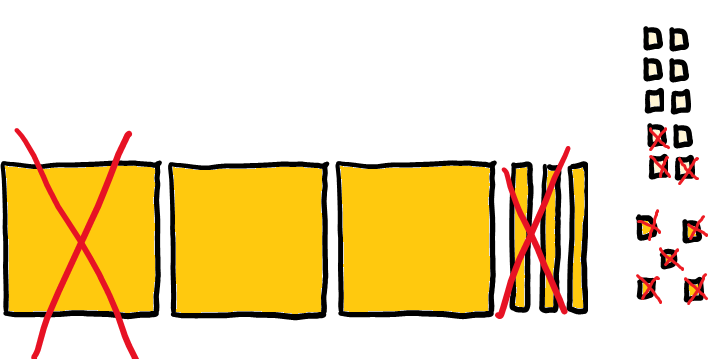
4. ¡Vaya rollo! ¿Todo eso para hacer una simple resta? “Todo esto” lo hacen durante un tiempo en fase concreta para garantizar que comprenden lo que hacen, para asegurarnos de que dominan lo que se conoce como sentido numérico. Después, escriben la resta de manera que concuerda con lo que hicieron sus manos. Escriben y verbalizan esta situación así:
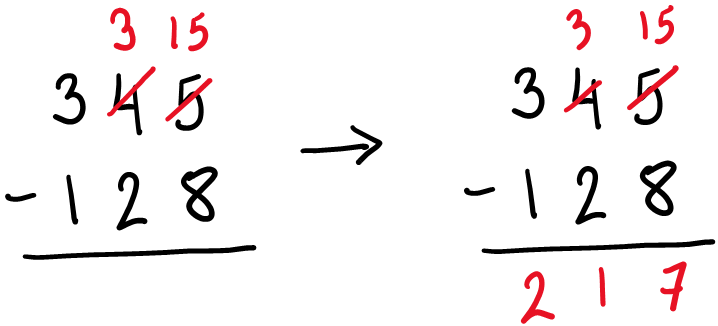
Ellos, antes de lanzarse a restar ya numéricamente, “preparan” la resta. Ven que a 5 unidades no le pueden quitar 8 pero saben que no tienen más que cambiar una decena por 10 unidades. De ese modo ya no tendrán 4 decenas sino 3 decenas, pero, a cambio, tendrán 15 unidades (y no 5). La resta está preparada y ya puedo quitar todo, todito lo que necesito (y, por supuesto, da igual que empecemos por la derecha, por la izquierda o por el centro).
Este proceso de cálculo “modernito” descrito y al que me he referido como “el trato justo”, no tiene nada de modernito y es aplicable a las 4 operaciones y a los decimales, y a las fracciones… No es más que trabajar desde la descomposición. En el caso anterior hemos pasado de ver el “trescientos cuarenta y cinco” como “trescientos treinta y quince” acomodando de ese modo la cantidad a la necesidad de ese momento. En este caso, quitarle “cien y veinte y ocho”: esto es el famoso sentido numérico.
En cualquier caso, el objetivo que se pretendía en nuestros tiempos “egeberos” era el de hacer cálculos y más cálculos como si eso fuera sinónimo de saber mates y ser bueno en ellas. ¿Sabéis cuál es la mayor dificultad a nivel MUNDIAL (así con mayúsculas que impresiona más)? Pues no es el cálculo. De hecho, el cálculo es algo que se nos da bastante bien a los humanos del mundo (según indican, en general, las pruebas internacionales PISA y TIMSS). El problema, y valga la redundancia, son los problemas.